| |
|
|
|
|
The algorithms of evaluating transcendental functions are based on mathematically
rigorous analysis of all kinds of numerical errors including iterative,
truncation and round-off errors. They guarantee that the final result has NBIT
correct bits of mantissa for both real and complex parts, where NBIT is a user-specified
parameter (please see the documentation). In order to make sure that ExLAF77 actually provides
that feature for any input values of arguments, a set of massive thorough tests has been performed
including systematic comparison of results computed with different precision, and comparison
with respective calculations by an independent multiprecision library.
During test phase, each output result is treated as a correct one only if it appeares
to be valid up to the NBIT-th bit of significand. Particular attention is paid to verification
of resulting accuracy for big values of arguments and in the vicinity of singular points.
If you need guaranteed resulting accuracy of vector-matrix operations, this is easily achieved
by means of specific organization of the calling program. You arrange a loop of
repeated computations with incrementally increasing lengths of floating point number
representations until resulting values converge to the desired accuracy.
|
|
It is object-oriented because it provides a whole hierarchy of object types
with functionality ("methods") inherited down the tree. For example, any
operation that can be done with a square matrix, such as calculating LU
decomposition, is automatically available for Hermitian matrix (which is
derived from square matrix).
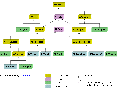
|
Click on this thumbnail to view the hierarchy chart for numbers
(the link will open in a new window).
Hierarchies for linear algebra objects, as well as detailed explanation of these
charts, can be found in
User's Manual (pp. 10 - 24).
|
|
|
- signed and unsigned infinities;
- short (4-byte) and arbitrarily long signed Integer numbers;
- arbitrarily long signed rational numbers;
- single (4-byte) and double (8-byte) precision real and complex floating-point numbers;
- arbitrarily long real and complex floating-point numbers;
- dense real and complex vectors represented as uniform arrays of single or double precision floating-point numbers;
- dense real and complex vectors represented as uniform arrays of arbitrarily long floating-point numbers;
- dense real and complex square and rectangular matrices represented as uniform arrays of floating-point numbers of the same kinds;
- dense real and complex Hermitian matrices represented as uniform arrays of floating-point numbers of the same kinds and stored in a packed form;
- complete triangular decompositions of general real and complex square matrices in the same representations;
- complete triangular decompositions of real and complex positive-definite and indefinite Hermitian matrices in the same representations;
- Hessenberg forms of general real and complex square matrices in the same representations;
- tridiagonal forms of real and complex positive-definite and indefinite Hermitian matrices in the same representations.
|
|
Yes. ExLAF77 data objects can be written as binary stream
to any file (e.g. on disk) and read later. These objects retain their validity
also in another session. It is possible because ExLAF77 objects are stricly
self-contained and location-independent.
|
|
The library is primarily intended to be called from Fortran-77 applications
(and Fortran-90/95 that include 77 standard). In particular, most routines
provide alternative return label arguments. In addition, C interface for
ExLAF77 is available, with Fortran's alternative return feature replaced by
returning completion status.
|
|
GNUmp imposes no limit on size of mantissa / integer besides computer's
physical memory, which allows GNUmp to be used for problems of computational number theory.
In ExLAF77, the maximum size of mantissa is 231 bits (or 256 Megabytes).
The limit on size of exponent in floating-point numbers in ExLAF77 is 231 bits
(or 256 Megabytes), and in GNUmp it is one machine word (i.e. 4 or 8 bytes).
Unlike GNUmp, ExLAF77 is
object-oriented in nature, so you always program for as generic types as possible.
|
|
- increased performance of most operations;
- more operations with floating point numbers;
- more operations with generic numbers;
- more operations with matrices
- polynomial one-argument functions
|
|
|
